Krzywa kalibracyjna krok po kroku
Większość laboratoriów wykorzystuje krzywą kalibracyjną do codziennych pomiarów. Jest więc rzeczą naturalną, że przy tej okazji pojawia się szereg pytań odnośnie wyznaczania jej parametrów i sposobów sprawdzania jakości uzyskanej krzywej. Dlatego też, celem niniejszego artykułu jest przeprowadzenie czytelnika, przez wyznaczenie parametrów krzywej kalibracyjnej, a następnie sprawdzenie jej jakości.
Definicja
W nowym wydaniu „Międzynarodowego słownika metrologii” nie ma pojęcia „krzywa kalibracyjna”. Chcąc operować pojęciami zgodnymi ze słownikiem należało by używać terminu „krzywa wzorcowania”. Problem jednak w tym, że wśród chemików zakorzeniło się sformułowanie „krzywa kalibracyjna”, które nie jest używane w praktyce.
Wracając do sedna sprawy, krzywa kalibracyjna to: „wyrażenie zależności pomiędzy wskazaniem, a odpowiadającą mu zmierzoną wartością wielkości”. Innymi słowy, wyznaczenie parametrów krzywej kalibracyjnej ma umożliwić przekształcenie wskazania urządzenia pomiarowego, na wartość zmierzoną. Posługując się przykładem analizy chromatograficznej, dzięki wyznaczeniu parametrów krzywej kalibracyjnej można zamienić pole powierzchni, na stężenie danego składnika w badanej mieszaninie.
Wyznaczanie parametrów krzywej kalibracyjnej (krzywej wzorcowania)
Po krótkim wstępie, wiadomo już do czego potrzebna jest krzywa kalibracyjna, w związku z czym pokażę teraz, jak wyznaczyć parametry charakteryzujące krzywą kalibracyjną.
KROK I – zbierz dane
W kroku I niezbędne jest zebranie danych, potrzebnych do dalszych obliczeń. Jeśli w laboratorium pierwszy raz przygotowuje się krzywą kalibracyjną dla konkretnego urządzenia pomiarowego, pojawia się problem, który polega na tym, że nie wiadomo, jakiego rozrzutu wyników spodziewać się dla konkretnych punktów pomiarowych.
Na szczęście norma PN-EN ISO 6143 „Analiza gazu. Metody porównawcze do określenia i sprawdzania składu gazowych mieszanin wzorcowych” podpowiada w ilu punktach pomiarowych należy przeprowadzić wzorcowanie, i w zależności od tego jaką funkcję matematyczną wybrać do opisu krzywej kalibracyjnej.
Jeżeli krzywa kalibracyjna ma być określona funkcją liniową, to norma PN-EN ISO 6143 zaleca minimum trzy punkty kalibracyjne. Wynika to z bardzo prostego założenia. Otóż dwa punkty potrzebne są do tego, aby wyznaczyć równanie prostej, z którego odczytuje się współczynniki a i b dla krzywej kalibracyjnej. Z kolei trzeci punkt ma na celu potwierdzić, że charakterystyka odpowiedzi układu pomiarowego na wzrastające stężenie analitu jest liniowa.
Korzystając z faktu, że większość krzywych kalibracyjnych wykorzystywanych w laboratoriach ma charakter liniowy, omówię wyznaczanie parametrów krzywej kalibracyjnej właśnie w modelu liniowym. W tym celu konieczne będzie wykonanie przynajmniej trzech pomiarów w każdym z trzech punktów kalibracyjnych. Najlepiej jednak wykonać minimum pięć pomiarów w każdym punkcie, aby móc odrzucić ewentualne wyniki odstające, a ze statystycznego punktu widzenia dziesięć pomiarów to absolutne minimum.
W laboratorium w którym pracuję wykonujemy dwanaście pomiarów dla każdego punktu wzorcowania. Dzięki takiemu podejściu, nawet jeżeli zdarzy się jeden wynik odstający to i tak mamy ponad dziesięć wyników pomiarów do dalszych obliczeń, a więc od strony statystycznej jest to bardzo dobra reprezentacja zbioru danych.
KROK II – wyznaczenie parametrów charakteryzujących krzywą kalibracyjną
Wyznaczanie parametrów krzywej kalibracyjnej najlepiej rozpocząć od wyznaczenia współczynnika zmienności, dla każdego z punktów wzorcowania. Jest to bardzo istotny parametr, ponieważ od niego zależy czy wyznaczona krzywa kalibracyjna będziesz użyteczna w pełnym zakresie pomiarowym oraz czy będzie konieczne podzielenie jej na podzakresy, a co się z tym wiąże czy dla każdego z podzakresów wykonanie dodatkowych pomiarów w punktach wzorcowania, tak aby w każdym podzakresie były przynajmniej trzy punkty wzorcowania.
Wzór do obliczenia współczynnika zmienności:
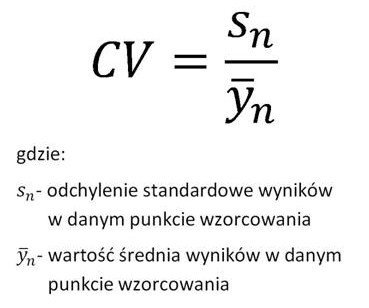
W celu statystycznej oceny różnic współczynników zmienności dla poszczególnych punktów wzorcowania można wykorzystać test F-Snedecora:
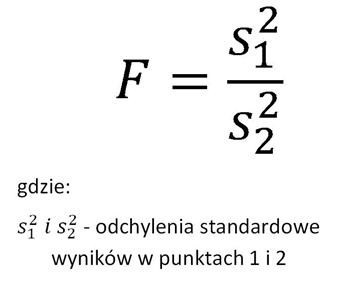
Przy czym warunkiem przeprowadzenia testu jest, aby odchylenie standardowe w liczniku miało większą wartość, niż odchylenie standardowe w mianowniku i wtedy jeżeli wyliczona wartość testu jest większa, od wartości tablicowej, uznaje się, że różnice odchyleń standardowych w poszczególnych punktach wzorcowania są statystycznie nieistotne.
Jeżeli porównanie trzech punktów wzorcowania parami wykaże brak różnic istotnych statystycznie, można wtedy przyjąć, że przedział roboczy krzywej kalibracyjnej determinowany jest przez najniższy i najwyższy punkt wzorcowania.
KROK III – wyznaczanie współczynników a i b
Znając zakres roboczy krzywej kalibracyjnej, można przejść do wyznaczania współczynników a i b funkcji liniowej opisującej równanie krzywej kalibracyjnej. W tym celu wykorzystać należy poniższe wzory:
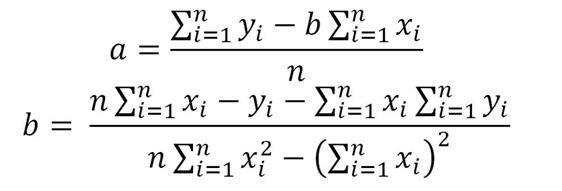
gdzie:
– współczynnik a, to wartość sygnału dla próbki ślepej,
– współczynnik b charakteryzuje czułość układu pomiarowego.
Oznacza to, że krzywa kalibracyjna ma postać y = a + bx.
Do wyznaczenia współczynników a i b można także wykorzystać popularny arkusz kalkulacyjny Excel. Formuły, które umożliwiają obliczenie tych współczynników to: „nachylenie” i „odcięta”. Arkusz kalkulacyjny Excel pozwala także na wyznaczenie odchylenia standardowego reszt S(z) – funkcja “REGBŁSTD” oraz współczynnika determinacji liniowej R2 – funkcja “R.KWADRAT”.
KROK IV – ocena jakości krzywej kalibracyjnej
Wspomniałem już o tym jak korzystając z arkusza kalkulacyjnego Excel wyznaczyć odchylenie standardowe reszt i współczynnik determinacji liniowej określone następującymi wzorami:
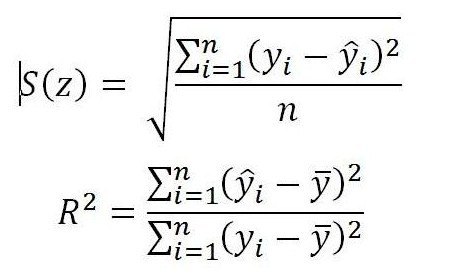
Wskaźniki te potrzebne są do oceny jakościowej krzywej kalibracyjnej. Odchylenie standardowe reszt określa o ile przeciętna wartość empiryczna odchyla się od wartości teoretycznej. Innymi słowy odchylenie standardowe reszt pokazuje jak duża jest różnica, pomiędzy teoretycznym położeniem punktów wzorcowania (wyznaczonym na podstawie parametrów krzywej kalibracyjnej), a faktycznym położeniem punktów zarejestrowanym w trakcie pomiarów.
Im wartość S(z) jest niższa, tym lepsze dopasowanie krzywej kalibracyjnej do punktów wzorcowania. Niestety odchylenie standardowe reszt nie jest wartością znormalizowaną, co w praktyce oznacza, że nie może być wykorzystane do oceny dwóch różnych krzywych kalibracyjnych.
Jeżeli jednak w laboratorium istnieje potrzeba wykorzystania tego parametru do porównania dwóch krzywych kalibracyjnych można wykorzystać wzór standaryzowany, który ma następującą postać:
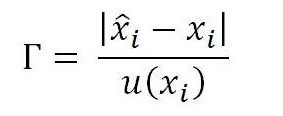
Konieczne jest wyznaczenie takiego odchylenia dla każdego punktu, a następnie upewnienie się, że maksymalna wartość . Można również porównywać maksymalne wartości pomiędzy różnymi krzywymi kalibracyjnymi.
Współczynnik determinacji liniowej R2 jest wartością znormalizowaną i przyjmuje wartości z przedziału <0;1>. Im wartość R2 sytuuje się bliżej 1 tym lepsze jest dopasowanie krzywej do punktów empirycznych. Współczynnik determinacji liniowej może również służyć do porównywania krzywych między sobą.
Warto zawsze ocenić wizualnie dopasowanie krzywej do punktów kalibracyjnych, dlatego że wskaźniki matematyczne nie wyeliminują subtelnych błędów, takich jak dopasowanie krzywej kalibracyjnej opisanej funkcją liniową do punktów układających się w kształcie paraboli. Z matematycznego punktu widzenia część punktów układa się nad krzywą, część pod i wskaźniki matematyczne nie sygnalizują problemu, który można zaobserwować empirycznie.
KROK V – wyznaczenie zakresu roboczego krzywej kalibracyjnej
Przy wyznaczaniu zakresu roboczego krzywej kalibracyjnej warto pamiętać o dobrej praktyce, która mówi, że zakres ten powinien znajdować się pomiędzy zawartością analitu w najniższym wzorcu odniesienia, a zawartością analitu w najwyższym wzorcu odniesienia. Dzięki takiemu ograniczeniu zakresu roboczego można mieć pewność, że odpowiedź układu pomiarowego jest dobrze zbadana w interesującym nas zakresie.
Drugim elementem, który należy wziąć pod uwagę podczas wyznaczania zakresu roboczego jest współczynnik zmienności CV. Dla każdego z punktów kalibracyjnych znajdujących się w zakresie roboczym współczynnik zmienności powinien być na tym samym poziomie, co można sprawdzić na przykład testem F-Snedecora. Wzory, które należy wykorzystać do obliczeń zawarte są w tej publikacji.
W procesie wyznaczania zakresu roboczego można także określić granicę wykrywalności i oznaczalności danego analitu na konkretnym układzie pomiarowym z wykorzystaniem analizowanej krzywej kalibracyjnej. Do tego celu służą dwa wzory w zależności od tego, czy dysponujemy wynikami analiz ślepej próby (ta metoda jest zalecana), czy nie.
Metoda I
yI = yśp + psśp
gdzie:
yI – sygnał analityczny odpowiadający granicznemu stężeniu CI
yśp – średni sygnał uzyskany dla ślepej próby
p – stała
sśp – odchylenie standardowe dla ślepej próby
Metoda II
yI = b + psb
gdzie:
yI – sygnał analityczny odpowiadający granicznemu stężeniu CI
b – współczynnik przecięcia
p – stała
sb – odchylenie standardowe współczynnika przecięcia
W zależności od tego, czy określona ma być granica wykrywalności, czy granica oznaczalności, stała p przyjmuje odpowiednio wartości 3 lub 10. Obie te wartości mają swoje statystyczne uzasadnienie, które zapewnia, że z określonym prawdopodobieństwem sygnał pochodzi od badanego analitu i można na jego podstawie jakościowo i ilościowo określić zawartość analitu w badanej próbce.
KROK VI – bieżąca kontrola użyteczność krzywej kalibracyjnej
Bieżąca kontrola zmienności parametrów krzywej kalibracyjnej ma na celu zapewnić, że parametry te nie uległy zmianie bardziej niż to wynika z charakterystyki danej metody. W tym celu zaleca się wykorzystanie zestawu przynajmniej trzech materiałów odniesienia. Mogą to być materiały już wykorzystane do kalibracji, lub nowy zestaw materiałów odniesienia. Ważne jest, aby zestaw ten pokrywał cały zakres roboczy, najlepiej w punktach ok. 10%, 50% i 90% zakresu roboczego.
W praktyce można też wykorzystać dowolny materiał pod warunkiem, że matryca jest podobna do matrycy spotykanej w badaniach rutynowych oraz że jest to materiał o znanej i odpowiednio długiej stabilności. Przykładowo, jeżeli planujemy kalibrację układu pomiarowego co sześć miesięcy, dobrze by było aby stabilność materiału służącego do kontroli była przynajmniej dwukrotnie dłuższa. W innym wypadku nie będzie wiadomo, czy niekorzystny trend, lub przekroczenie linii kontrolnych na kartach kontrolnych pochodzi od układu pomiarowego, czy od materiału stosowanego do kontroli.
Mając wybrany materiał do kontroli bieżącej należy wykonać dziesięć analiz celem wyznaczenia wartości średniej, która stanie się linią centralną na karcie kontrolnej oraz odchylenia standardowego, które posłuży do wyznaczania linii kontrolnych. Wewnętrzna linia kontrolna to dwukrotne odchylenie standardowe, a zewnętrzna linia kontrolna to trzykrotne odchylenie standardowe.
Prowadząc karty kontrolne należy zwrócić uwagę na:
– przekroczenia wewnętrznej linii kontrolnej, które jeśli zdarzają się często (więcej niż 5 przypadków na 100 pomiarów) należy traktować jako sygnał ostrzegawczy;
– przekroczenia zewnętrznej linii kontrolnej, które każdorazowo należy traktować jak sygnał ostrzegawczy;
– układania się wyników w niekorzystny trend, zmierzający do przekroczenia linii kontrolnych, lub mający tendencję do zaniżania, lub zawyżania wyników.
Zaletą prowadzenia kart kontrolnych jest to, że doświadczony analityk na podstawie tych kart potrafi odpowiednio wcześniej wychwycić sytuacje potencjalnie niebezpieczne dla wyników prowadzonych badań. Ponadto karty kontrolne pomagają przy rewalidacji metody pomiarowej, gdyż na ich podstawie łatwo można oszacować, czy metoda nadal zachowuje swoją charakterystykę wyznaczoną w trakcie pierwszej walidacji.
Podsumowanie
Przedstawiłem wszystkie niezbędne informacje potrzebne do pracy z krzywą kalibracyjną. Jednak nie wyczerpują one w pełni zagadnień związanych z praktycznym zastosowaniem krzywej kalibracyjnej w laboratorium. Niemniej zastosowanie opisanych tu metod pozwoli na przeprowadzenie sprawnej kalibracji układu pomiarowego, a następnie skutecznego monitorowania charakterystyki układu pomiarowego.
*mgr Krzysztof Nyrek – chemik, metrolog; krzysztof.nyrek@gmail.com(link sends e-mail)
Prezentacja tematu: http://www.youtube.com/watch?v=AG5MgigDSJA
